with properties of space that are related with distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a .
Until the 19th century, geometry was almost exclusively devoted to , which includes the notions of , , , , , , and , as fundamental concepts.
During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is ‘ (remarkable theorem) that asserts roughly that the of a surface is independent from any specific in an . This implies that surfaces can be studied intrinsically, that is as stand alone spaces, and has been expanded into the theory of and .
Later in the 19th century, it appeared that geometries without the () can be developed without introducing any contradiction. The geometry that underlies is a famous application of non-Euclidean geometry.
Since then, the scope of geometry has been greatly expanded, and the field has been split in many subfields that depend on the underlying methods, , , , (also known as combinatorial geometry), etc.or on the properties of Euclidean spaces that are disregarded that consider only alignment of points but not distance and parallelism, that omits the concept of angle and distance, that omits , etc.
Often developed with the aim to model the physical world, geometry has applications to almost all , and also to , , and other activities that are related to . Geometry has also applications to areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental for of , a problem that was stated in terms of , and remained unsolved for several centuries.
Contents
History
Main article: 
A and an practicing geometry in the 15th century
The earliest recorded beginnings of geometry can be traced to ancient and in the 2nd millennium BC. Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in , , , and various crafts. The earliest known texts on geometry are the (20001800 BC) and (c. 1890 BC), the such as (1900 BC). For example, the Moscow Papyrus gives a formula for calculating the volume of a truncated pyramid, or . Later clay tablets (35050 BC) demonstrate that Babylonian astronomers implemented procedures for computing Jupiter’s position and within time-velocity space. These geometric procedures anticipated the , including the , by 14 centuries. South of Egypt the established a system of geometry including early versions of sun clocks.
In the 7th century BC, the mathematician used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to . Pythagoras established the , which is credited with the first proof of the , though the statement of the theorem has a long history. (408c. 355 BC) developed the , which allowed the calculation of areas and volumes of curvilinear figures, as well as a theory of ratios that avoided the problem of , which enabled subsequent geometers to make significant advances. Around 300 BC, geometry was revolutionized by Euclid, whose , widely considered the most successful and influential textbook of all time, introduced through the and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the Elements were already known, Euclid arranged them into a single, coherent logical framework. The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today. (c. 287212 BC) of used the to calculate the under the arc of a with the , and gave remarkably accurate approximations of . He also studied the bearing his name and obtained formulas for the of .
Woman teaching geometry. Illustration at the beginning of a medieval translation of , (c. 1310).
mathematicians also made many important contributions in geometry. The (3rd century BC) contains rules for ritual geometric constructions that are similar to the . According to (, p. 363), the ulba Stras contain “the earliest extant verbal expression of the Pythagorean Theorem in the world, although it had already been known to the Old Babylonians. They contain lists of , which are particular cases of . In the , there is a handful of geometric problems (including problems about volumes of irregular solids). The Bakhshali manuscript also “employs a decimal place value system with a dot for zero.” ‘s (499) includes the computation of areas and volumes. wrote his astronomical work in 628. Chapter 12, containing 66 verses, was divided into two sections: “basic operations” (including cube roots, fractions, ratio and proportion, and barter) and “practical mathematics” (including mixture, mathematical series, plane figures, stacking bricks, sawing of timber, and piling of grain). In the latter section, he stated his famous theorem on the diagonals of a . Chapter 12 also included a formula for the area of a cyclic quadrilateral (a generalization of ), as well as a complete description of (i.e. triangles with rational sides and rational areas).
In the , contributed to the development of geometry, especially . (b. 853) conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra. (known as Thebit in ) (836901) dealt with operations applied to of geometrical quantities, and contributed to the development of . (10481131) found geometric solutions to . The theorems of (Alhazen), Omar Khayyam and on , including the and , were early results in , and along with their alternative postulates, such as , these works had a considerable influence on the development of non-Euclidean geometry among later European geometers, including (c. 1230c. 1314), (12881344), , , and .[ ]
In the early 17th century, there were two important developments in geometry. The first was the creation of analytic geometry, or geometry with and , by (15961650) and (16011665). This was a necessary precursor to the development of and a precise quantitative science of . The second geometric development of this period was the systematic study of by (15911661). Projective geometry studies properties of shapes which are unchanged under and , especially as they relate to .
Two developments in geometry in the 19th century changed the way it had been studied previously. These were the discovery of by Nikolai Ivanovich Lobachevsky, Jnos Bolyai and Carl Friedrich Gauss and of the formulation of as the central consideration in the of (which generalized the Euclidean and non-Euclidean geometries). Two of the master geometers of the time were (18261866), working primarily with tools from , and introducing the , and , the founder of and the geometric theory of . As a consequence of these major changes in the conception of geometry, the concept of “space” became something rich and varied, and the natural background for theories as different as and .
Important concepts in geometry
The following are some of the most important concepts in geometry.
Axioms
An illustration of Euclid’s See also: and
took an abstract approach to geometry in his , one of the most influential books ever written. Euclid introduced certain , or , expressing primary or self-evident properties of points, lines, and planes. He proceeded to rigorously deduce other properties by mathematical reasoning. The characteristic feature of Euclid’s approach to geometry was its rigor, and it has come to be known as axiomatic or geometry. At the start of the 19th century, the discovery of by (17921856), (18021860), (17771855) and others led to a revival of interest in this discipline, and in the 20th century, (18621943) employed axiomatic reasoning in an attempt to provide a modern foundation of geometry.
Points
Main article:
Points are considered fundamental objects in Euclidean geometry. They have been defined in a variety of ways, including Euclid’s definition as ‘that which has no part’ and through the use of algebra or nested sets. In many areas of geometry, such as analytic geometry, differential geometry, and topology, all objects are considered to be built up from points. However, there has been some study of geometry without reference to points.
Lines
Main article:
described a line as “breadthless length” which “lies equally with respect to the points on itself”. In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in , a line in the plane is often defined as the set of points whose coordinates satisfy a given , but in a more abstract setting, such as , a line may be an independent object, distinct from the set of points which lie on it. In differential geometry, a is a generalization of the notion of a line to .
Planes
Main article:
A is a flat, two-dimensional surface that extends infinitely far. Planes are used in every area of geometry. For instance, planes can be studied as a without reference to distances or angles; it can be studied as an , where collinearity and ratios can be studied but not distances; it can be studied as the using techniques of ; and so on.
Angles
Main article:
defines a plane as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. In modern terms, an angle is the figure formed by two , called the sides of the angle, sharing a common endpoint, called the of the angle.
Acute (a), obtuse (b), and straight (c) angles. The acute and obtuse angles are also known as oblique angles.
In , angles are used to study and , as well as forming an object of study in their own right. The study of the angles of a triangle or of angles in a forms the basis of .
In and , the angles between or or can be calculated using the .
Curves
Main article:
A is a 1-dimensional object that may be straight (like a line) or not; curves in 2-dimensional space are called and those in 3-dimensional space are called .
In topology, a curve is defined by a function from an interval of the real numbers to another space. In differential geometry, the same definition is used, but the defining function is required to be differentiable Algebraic geometry studies , which are defined as of one.
Surfaces
Main article: 
A sphere is a surface that can be defined parametrically (by x = r sin cos , y = r sin sin , z = r cos ) or implicitly (by x2 + y2 + z2 r2 = 0.)
A is a two-dimensional object, such as a sphere or paraboloid. In and , surfaces are described by two-dimensional ‘patches’ (or ) that are assembled by or , respectively. In algebraic geometry, surfaces are described by .
Manifolds
Main article:
A is a generalization of the concepts of curve and surface. In , a manifold is a where every point has a that is to Euclidean space. In , a is a space where each neighborhood is to Euclidean space.
Manifolds are used extensively in physics, including in and .
Length, area, and volume
Main articles: , , and See also: , and
, , and describe the size or extent of an object in one dimension, two dimension, and three dimensions respectively.
In and , the length of a line segment can often be calculated by the .
Area and volume can be defined as fundamental quantities separate from length, or they can be described and calculated in terms of lengths in a plane or 3-dimensional space. Mathematicians have found many explicit and of various geometric objects. In , area and volume can be defined in terms of , such as the or the .
Metrics and measures
Main articles: and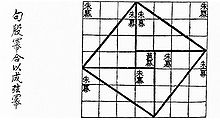 
Visual checking of the for the (3, 4, 5) as in the 500200 BC. The Pythagorean theorem is a consequence of the .
The concept of length or distance can be generalized, leading to the idea of . For instance, the measures the distance between points in the , while the measures the distance in the . Other important examples of metrics include the of and the semi- of .
In a different direction, the concepts of length, area and volume are extended by , which studies methods of assigning a size or measure to , where the measures follow rules similar to those of classical area and volume.
Congruence and similarity
Main articles: and
and are concepts that describe when two shapes have similar characteristics. In Euclidean geometry, similarity is used to describe objects that have the same shape, while congruence is used to describe objects that are the same in both size and shape. , in his work on creating a more rigorous foundation for geometry, treated congruence as an undefined term whose properties are defined by .
Congruence and similarity are generalized in , which studies the properties of geometric objects that are preserved by different kinds of transformations.
Compass and straightedge constructions
Main article:
Classical geometers paid special attention to constructing geometric objects that had been described in some other way. Classically, the only instruments allowed in geometric constructions are the and . Also, every construction had to be complete in a finite number of steps. However, some problems turned out to be difficult or impossible to solve by these means alone, and ingenious constructions using parabolas and other curves, as well as mechanical devices, were found.
Dimension
Main article: 
The , with =log4/log3 and =1
Where the traditional geometry allowed dimensions 1 (a ), 2 (a ) and 3 (our ambient world conceived of as ), mathematicians and physicists have used for nearly two centuries. One example of a mathematical use for higher dimensions is the of a physical system, which has a dimension equal to the system’s . For instance, the configuration of a screw can be described by five coordinates.
In , the concept of dimension has been extended from , to infinite dimension (, for example) and positive (in ). In , the has received a number of apparently different definitions, which are all equivalent in the most common cases.
Symmetry
Main article: 
A of the
The theme of in geometry is nearly as old as the science of geometry itself. Symmetric shapes such as the , and held deep significance for many ancient philosophers and were investigated in detail before the time of Euclid. Symmetric patterns occur in nature and were artistically rendered in a multitude of forms, including the graphics of , , and others. In the second half of the 19th century, the relationship between symmetry and geometry came under intense scrutiny. ‘s proclaimed that, in a very precise sense, symmetry, expressed via the notion of a transformation , determines what geometry is. Symmetry in classical is represented by and rigid motions, whereas in an analogous role is played by , that take straight lines into straight lines. However it was in the new geometries of Bolyai and Lobachevsky, Riemann, and Klein, and that Klein’s idea to ‘define a geometry via its ‘ found its inspiration. Both discrete and continuous symmetries play prominent roles in geometry, the former in and , the latter in and .
A different type of symmetry is the principle of in , among other fields. This meta-phenomenon can roughly be described as follows: in any , exchange point with plane, join with meet, lies in with contains, and the result is an equally true theorem. A similar and closely related form of duality exists between a and its .
Contemporary geometry
Euclidean geometry
Main article:
is geometry in its classical sense. As it models the space of the physical world, it is used in many scientific areas, such as , , , and many technical fields, such as , , , , and . The mandatory educational curriculum of the majority of nations includes the study of Euclidean concepts such as , , , , , , , , , and .
Differential geometry
uses tools from to study problems involving curvature.Main article:
uses techniques of and to study problems in geometry. It has applications in , , and , among others.
In particular, differential geometry is of importance to due to ‘s postulation that the is . Differential geometry can either be intrinsic (meaning that the spaces it considers are whose geometric structure is governed by a , which determines how distances are measured near each point) or extrinsic (where the object under study is a part of some ambient flat Euclidean space).
Non-Euclidean geometry
Main article:
Euclidean geometry was not the only historical form of geometry studied. has long been used by astronomers, astrologers, and navigators.
argued that there is only one, absolute, geometry, which is known to be true a priori by an inner faculty of mind: Euclidean geometry was . This view was at first somewhat challenged by thinkers such as , then finally overturned by the revolutionary discovery of in the works of Bolyai, Lobachevsky, and Gauss (who never published his theory). They demonstrated that ordinary is only one possibility for development of geometry. A broad vision of the subject of geometry was then expressed by in his 1867 inauguration lecture ber die Hypothesen, welche der Geometrie zu Grunde liegen (On the hypotheses on which geometry is based), published only after his death. Riemann’s new idea of space proved crucial in ‘s . , which considers very general spaces in which the notion of length is defined, is a mainstay of modern geometry.
Topology
Main article: 
A thickening of the
is the field concerned with the properties of , and can be considered a generalization of Euclidean geometry. In practice, topology often means dealing with large-scale properties of spaces, such as and .
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of , in which transformations are . This has often been expressed in the form of the saying ‘topology is rubber-sheet geometry’. Subfields of topology include , , and .
Algebraic geometry
Main article: 
Quintic
The field of developed from the of . It underwent periodic periods of growth, accompanied by the creation and study of , , , and , among other topics. From the late 1950s through the mid-1970s it had undergone major foundational development, largely due to work of and . This led to the introduction of and greater emphasis on methods, including various . One of seven , the , is a question in algebraic geometry. uses advanced methods of algebraic geometry for solving a long-standing problem of .
In general, algebraic geometry studies geometry through the use of concepts in such as . It has applications in many areas, including and .
Complex geometry
Main article:
studies the nature of geometric structures modelled on, or arising out of, the . Complex geometry lies at the intersection of differential geometry, algebraic geometry, and analysis of , and has found applications to and .
Complex geometry first appeared as a distinct area of study in the work of in his study of . Work in the spirit of Riemann was carried out by the in the early 1900s. Contemporary treatment of complex geometry began with the work of , who introduced the concept of to the subject, and illuminated the relations between complex geometry and algebraic geometry. The primary objects of study in complex geometry are , , and , and and over these spaces. Special examples of spaces studied in complex geometry include Riemann surfaces, and , and these spaces find uses in string theory. In particular, of strings are modelled by Riemann surfaces, and predicts that the extra 6 dimensions of 10 dimensional may be modelled by Calabi-Yau manifolds.
Discrete geometry
Main article: 
Discrete geometry includes the study of various .
is a subject that has close connections with . It is concerned mainly with questions of relative position of simple geometric objects, such as points, lines and circles. Examples include the study of , , the Kneser-Poulsen conjecture, etc. It shares many methods and principles with .
Computational geometry
Main article:
deals with and their for manipulating geometrical objects. Important problems historically have included the , , , and .
Although being a young area of geometry, it has many applications in , , , , etc.
Geometric group theory
Main article: 
The Cayley graph of the on two generators a and b
uses large-scale geometric techniques to study . It is closely connected to , such as in ‘s proof of the , which included the proof of the , a .
Geometric group theory often revolves around the , which is a geometric representation of a group. Other important topics include , , and .
Convex geometry
Main article:
investigates shapes in the Euclidean space and its more abstract analogues, often using techniques of and . It has close connections to , and and important applications in .
Convex geometry dates back to antiquity. gave the first known precise definition of convexity. The , a recurring concept in convex geometry, was studied by the Greeks as well, including . Archimedes, , , and later and all studied and their properties. From the 19th century on, mathematicians have studied other areas of convex mathematics, including higher-dimensional polytopes, volume and surface area of convex bodies, , , and .
Applications
Geometry has found applications in many fields, some of which are described below.
Art
Main article: 
Bou Inania Madrasa, Fes, Morocco, zellige mosaic tiles forming elaborate geometric tessellations
Mathematics and art are related in a variety of ways. For instance, the theory of showed that there is more to geometry than just the metric properties of figures: perspective is the origin of .
Artists have long used concepts of in design. developed a complicated theory of ideal proportions for the human figure. These concepts have been used and adapted by artists from to modern comic book artists.
The is a particular proportion that has had a controversial role in art. Often claimed to be the most aesthetically pleasing ratio of lengths, it is frequently stated to be incorporated into famous works of art, though the most reliable and unambiguous examples were made deliberately by artists aware of this legend.
, or tessellations, have been used in art throughout history. makes frequent use of tessellations, as did the art of . Escher’s work also made use of .
advanced the theory that all images can be built up from the , the , and the . This is still used in art theory today, although the exact list of shapes varies from author to author.
Architecture
Main articles: and
Geometry has many applications in architecture. In fact, it has been said that geometry lies at the core of architectural design. Applications of geometry to architecture include the use of to create , the use of in constructing domes and similar objects, the use of , and the use of symmetry.
Testimonials
